Te compartimos estos ejercicios, si querés practicar más:

• Ejercicios de matemática para estudiantes

• Ejercicios de Matemática - Módulo 1

• Ejercicios de Matemática - Módulo 2
• Ejercicios de Matemática - Módulo 3

Servicios generales y administrativos: módulo 1 unidad II sin potencia ni radicación, unidad III, unidad V.
Profesionales: módulo 1 unidad V, módulo 2 unidad 1 ecuaciones, unidad 4 funciones, módulo 3 unidad 3 proporcionalidad numérica, unidad 4 estadística descriptiva, unidad 5 proporcionalidad.

Tipo de examen: Servicios generales y administrativos

1. Velocidad de un auto de carrera
   Este gráfico muestra cómo varía la velocidad de un auto de carrera a lo largo de una pista plana de 3km durante su segunda vuelta.
   

   

   
   ¿Dónde se registró la velocidad más baja durante la segunda vuelta?
   A. En la línea de partida.
   B. Aproximadamente en el km 0.8.
   C. Aproximadamente en el km 1.3.
   D. A mitad del recorrido
   
   Respuesta: C
   En el eje vertical se puede observar la velocidad promedio del auto de carrera. Siendo la velocidad más baja del recorrido en aproximadamente 70 km/h a los aproximadamente 1.3 km.
   
   ¿Cuál es la distancia aproximada desde el punto donde se registró la velocidad mínima y la próxima vez que el auto desaceleró?
   A. 0.5 km
   B. 1 km
   C. 1.7 km
   D. 2.3 km
   
   Respuesta B
   Desde el punto donde se registró la velocidad más baja, 1.3 km hasta que se vuelve a reducir en 2.3 km hay un 1 km aproximadamente.
   
   Fuente: PISA, matemáticas, actividades de simulación.

2. Faro
   Los faros son torres provistas de una luz intermitente en su parte superior. Los faros ayudan a los barcos a encontrar su camino de noche, cuando navegan cerca de la costa.
   La luz de un faro se prende y se apaga respondiendo a un patrón fijo. Cada faro tiene su propio patrón.
   En el siguiente diagrama, se muestra el patrón de un determinado faro. Los rayos de luz se alternan con momentos de oscuridad.
   Éste es un patrón que se repite cada cierto tiempo. El tiempo que toma un ciclo completo, antes de comenzar a repetirse, se llama período. Cuando encuentras el período de un patrón, resulta fácil completar el diagrama para los siguientes segundos, o minutos, o incluso horas.
   

   

   
   ¿Cuál de los siguientes podría ser el período del patrón de este faro?
   A. 2 segundos
   B. 3 segundos
   C. 5 segundos
   12 segundos
   
   Respuesta: C
   Desde el segundo cero hasta que se repite la secuencia pasan 5 segundos.
   
   En el transcurso de un minuto ¿durante cuántos segundos emite rayos de luz este faro?
   A. 4
   B. 12
   C. 20
   D. 24
   
   Respuesta: D
   Un minuto tiene 60 segundos. En 10 segundos el faro emite rayos de luz por 4 segundos. Para obtener en un minuto cuántos segundos de emisión de rayos de luz hay se multiplica 4x6 y obtenemos 24 segundos de luz en un minuto.
   
   Fuente: PISA, matemáticas, actividades de simulación.

3. Los dados son cubos especiales con números, para los cuales se aplica la siguiente regla: el número total de puntos en dos caras opuestas siempre suma siete.
   

   

   
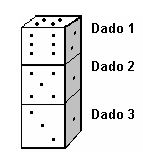
   En el dibujo de arriba, se ven tres dados apilados uno sobre otro. El dado 1 tiene 4 puntos en la cara de arriba.
   
   ¿Cuántos puntos hay en total en las cinco caras horizontales que no podés ver (cara de abajo del dado 1 y cara de arriba y de abajo de los dados 2 y 3)?
   A. 15
   B. 16
   C. 17
   D. 18
   
   Respuesta C
   Teniendo en cuenta que las caras opuestas suman 7, en el dado 1 la cara de abajo es 3, ya que 4+3 =7. En el dado 2 las caras de arriba y abajo son 4 y 3, ya que las que podemos ver son 6 y 1 por un lado y 5 y 3 por el otro, ya que ambos suman 7. Por último en el dado 3, caras de arriba y de abajo son el 5 y 2, ya que vemos la cara con 1 punto que su opuesto es 6 y la de 3 puntos que su opuesto es 4. Por lo tanto: sumando los puntos de las caras horizontales que no podemos ver obtenemos: 3+4+4+5+2 =17
   
   Fuente: PISA, matemáticas, actividades de simulación.

4. Roberto construye un patrón de escalones usando cuadrados. Estas son las etapas que sigue. Como puedes ver, él utiliza un cuadro en la etapa 1, tres cuadros en la etapa 2 y seis en la etapa 3.
   

   

   
   
   ¿Cuántos cuadrados debería usar en total para la etapa 4?
   A. 8
   B. 10
   C. 11
   D. 12
   
   Respuesta: B. El patrón va agregando una columna con cada vez más cuadrados en el lado izquierdo. La etapa 4 va a ser igual a la etapa 3 más 4 cuadrados más en una nueva columna a la izquierda. En total van a ser 10 cuadrados.
   
   Fuente: PISA, matemáticas, actividades de simulación.

5. La estatura promedio de los jóvenes hombres y mujeres de Holanda en 1998 está representada en el siguiente gráfico
   

   

   
   Desde 1980 hasta 1998 la estatura promedio de las mujeres de 20 años ha aumentado 2,3 cm, hasta alcanzar los 170,6 cm. ¿Cuál era la estatura promedio de las mujeres de 20 años de edad en 1980?
   A. 168,3 cm
   B. 171,6 cm
   C. 166,4 cm
   D. 160,5 cm
   
   Respuesta: A.
   Altura promedio en 1998 - Altura promedio en 1980 = Cambio
   170,6 cm - Altura promedio en 1980 = 2,3 cm
   170,6 cm - 2,3 cm = Altura promedio en 1980
   168,3 cm = Altura promedio en 1980
   
   Fuente: PISA, matemáticas, actividades de simulación.

6. El diagrama que está a continuación, muestra una escalera de 14 escalones y una altura total de 252 cm.
   

   

   
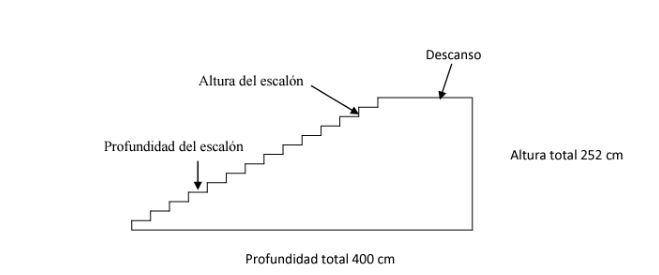
   ¿Cuál es la altura de cada uno de los 14 escalones?
   A. 18
   B. 20
   C. 22
   D. 25
   
   Respuesta A
   La altura total es de 252 cm si tengo 14 escalones debo dividir la altura total por 14 y obtengo que cada cada escalón tiene una altura de 18 cm.
   
   La figura de la escalera muestra a qué se refieren los términos profundidad del escalón y altura del escalón. Una escalera bien hecha debería construirse según la “fórmula para escaleras” que se describe en el siguiente recuadro
   

   

   
   La profundidad de los escalones depende de la altura de los escalones, y viceversa. Para calcular la profundidad o la altura, podés aplicar la “fórmula para escaleras”
   
   2 alturas de escalón + 1 profundidad de escalón = 63 cm.
   
   ¿Cuál debería ser la profundidad del escalón cuando la altura del escalón es 14 cm?
   A. 33
   B. 36
   C. 35
   D. 37
   
   Respuesta: C
   Sabemos que la altura del escalón es 14, por lo cual, podemos meter este valor en la “fórmula para escaleras”:
   2 x 14 cm + 1 profundidad de escalón = 63 cm.
   28 cm + 1 profundidad de escalón = 63 cm.
   1 profundidad de escalón = 63 cm - 28 cm
   1 profundidad de escalón = 35 cm
   
   Fuente: PISA, matemáticas, actividades de simulación.

7. x, 2x, 4x
   El primer término en la secuencia de arriba es x, y los términos subsiguientes son iguales al doble del anterior. ¿Cuál es la suma de los 5 primeros términos de la secuencia?
   A. 10x
   B. 15x
   C. 30x
   D. 31x
   
   Respuesta: D. Primero hay que encontrar los primeros 5 términos de la secuencia. Ya tenemos x, 2x, 4x. Los siguientes dos tienen que seguir cumpliendo la regla de que los términos subsiguientes sean el doble que el anterior, por lo que el 4to término es 8x, y el 5to término es 16x.
   x + 2x + 4x + 8x + 16x = 31x
   
   Fuente: Erikthered, SAT examen de práctica sección matemática nivel fácil

8. Un número es dividido por 4. Ese resultado es dividido por 4, llegando al resultado final de 2. ¿Cuál fue el número original?
   A.2
   B.8
   C.16
   D.32
   
   Respuesta: D.
   Si tomo el 2 y lo multiplico dos veces por 4, llego al valor inicial. Por ende, el número inicial es 2 x 4 x 4 = 32.
   
   Fuente: College Board, examen de práctica SAT matemáticas.

9. abcdeabcdeabc…
   En la siguiente secuencia de letras la primera letra es la a, seguida de la b, c, d y e. Luego el patrón vuelve a repetirse. ¿Cuál de las siguientes letras ocupa el lugar 31 en la secuencia?
   A. a
   B. b
   C. c
   D. d
   E. e
   
   Respuesta: A. Se ve que a cada 5 letras se repite el patrón. Por ende, la primera letra va a ser igual a la sexta, a la undécima, la decimosexta, la vigesimoprimera, la vigesimosexta y la trigesimoprimera. Por ende, la letra “a” ocupa el lugar 31 de la secuencia.
   
   Fuente: Erikthered, SAT examen de práctica sección matemática nivel fácil

10. Un granjero puede recoger 12 repollos en una hora. Trabajando al mismo ritmo ¿cuántas horas le llevaría a 2 granjeros recoger 48 repollos?
    A.1
    B.2
    C.4
    D.6
    
    Respuesta: B. Si un granjero recoge 12 repollos en una hora, 2 granjeros recogen el doble, es decir, 24. Al mismo ritmo, en 2 horas recogerán 48 repollos.
    
    Fuente: Erikthered, SAT examen de práctica sección matemática nivel fácil

11. El mes de Julio tiene 31 días ¿Cuál es la cantidad máxima de sábados que puede tener Julio?
    A:2
    B.3
    C.4
    D.5
    
    Respuesta: D.
    Necesitas saber que la semana tiene siete días, lo que significa que después de 28 días, han habido 4 sábados. De los 3 días extras uno podría ser un sábado.
    
    Fuente: Erikthered, SAT examen de práctica sección matemática nivel fácil

12. Patricia es 27 años más grande que Maximiliano, que es 38 años más jóven que Guillermo. ¿En cuantos años Patricia tendrá la edad que Guillermo tiene ahora?
    A.11
    B.10
    C.9
    D.13
    
    Respuesta: A. Como Guillermo es 38 años más grande que Maximiliano, y Patricia es 27 años más grande que Maximiliano, Guillemo es 11 años más grande que Patricia.
    
    Fuente: Erikthered, SAT examen de práctica sección matemática nivel fácil

13. Luis camina 600 metros en 10 minutos. Caminando al mismo ritmo ¿cuántos metros puede caminar en 10 segundos?
    A.4
    B.5
    C.10
    D.12
    
    Respuesta: C. Si hace 600 metros en 10 minutos, hace 60 metros por minuto. Como hay 60 segundos en un minuto, hace 1 metro por segundo. En 10 segundos hace 10 metros.
    
    Fuente: Erikthered, SAT examen de práctica sección matemática nivel fácil

14. Todos los repollos son rojos
    A. ¿Cuál de las siguientes afirmaciones muestra que la afirmación es falsa?
    B. Cecilia está comiendo una manzana verde
    C. Theo no está comiendo un repollo rojo
    D. Valentín está comiendo un repollo verde

Respuesta: D. Si Valentín está comiendo un repollo verde, no todos los repollos son rojos.

Fuente: Erikthered, SAT examen de práctica sección matemática nivel fácil

15. 2 árboles de pino crecen perpendiculares a un suelo liso. Uno de los 2 árboles mide 10 metros y tiene una sombra de 5 metros. Al mismo tiempo, la sombra del otro árbol es de 2 metros. ¿Cuán alto es, en metros, el otro árbol?
    A. 3
    B. 4
    C. 8
    D. 27
    
    Respuesta: B
    Como el suelo es liso y no hay inclinaciones, al ser la sombra del primer árbol la mitad de su altura podemos asumir lo mismo del segundo. Por lo cual, si la sombra es 2 metros su doble es 4 metros, siendo 4 la altura del árbol.
    
    Fuente: College Board, examen de práctica SAT matemáticas.

16. De 300 semillas que se plantaron, brotaron más de la mitad. ¿Qué total de semillas pudieron haber brotado?
    A. 20
    B. 140
    C. 250
    D. 320
    
    Respuesta: C. 20 y 140 son menos que la mitad, por lo cual no podrían ser el total. 320 es más que el total de semillas, por lo que la única respuesta correcta es 250.
    
    Fuente: College Board, examen de práctica SAT matemáticas.

17. Un cliente gastó $27 en comprar naranjas a $3 cada una. ¿Cuántas naranjas compró?
    A. 9
    B. 6
    C. 7
    D. 8
    
    Respuesta: A. 27 dividido 3 es 9.
    
    Fuente: College Board, examen de práctica SAT matemáticas.

18. Un grupo de estudiantes votó 5 actividades para realizar después de clases. El gráfico de barras muestra el número de estudiantes que votó cada una de las 5 actividades ¿Cuántos estudiantes eligieron la actividad 3?
    

    

    
    A. 25
    B. 39
    C. 48
    D. 50
    
    Respuesta: B. La barra está arriba de 35, abajo de 40. Todas las demás opciones no están en ese rango.
    
    Fuente: College Board, examen de práctica SAT matemáticas.

19. 13 es el valor p% de 25. ¿Cuál es el valor de p?
    A. 50
    B. 49
    C. 51
    D. 52
    
    Respuesta: D. 13 dividido 25 es 0.52. Es decir, 13 es el 52% de 25.
    
    Fuente: College Board, examen de práctica SAT matemáticas.

20. ¿Qué longitud, en centímetros, equivale a una longitud de 51 metros?
    (1 metros = 100 centimetros)
    A. 0,051
    B. 0,51
    C. 5.100
    D. 51.000
    
    Respuesta: C. 51 x 100 = 5.100
    
    Fuente: College Board, examen de práctica SAT matemáticas.

Tipo de examen: Profesionales

1. La tabla resume la distribución de colores y formas de 100 azulejos de igual área.
   

   

   
   Si se elige un azulejo de manera aleatoria, ¿cuál es la posibilidad de seleccionar un azulejo rojo?
   A. 3/10
   B. 2/8
   C. 4/10
   D. ⅝
   
   Respuesta: A. De los 100 azulejos totales, 30 son rojos (10 de ellos son cuadrados y 20 son pentágonos). La probabilidad se mide como casos que cumplen la afirmación dividido casos totales, es decir, 30/100. Simplificado, es 3/10.
   
   Fuente: College Board, examen de práctica SAT matemáticas.

2. De una población de 50.000 personas, 1000 fueron seleccionadas aleatoriamente y encuestadas sobre un proyecto de ley. Basada en la encuesta se estima que el 35% de la población apoya el proyecto de ley, con un margen de error del 3%. Basado en estos resultados, ¿cuál de los siguientes valores es más plausible para el total de la población que apoya el proyecto de ley?
   A. 350
   B. 650
   C. 16.750
   D. 31.760
   
   Respuesta: C.
   Se establece que aproximadamente el 35% de las personas en la población apoyan la legislación, con un margen de error asociado del 3%. Al restar y sumar el margen de error a la estimación, se obtiene un intervalo de valores plausibles para el porcentaje real de personas en la población que apoyan la legislación. Por lo tanto, es plausible que entre el 32% y el 38% de las personas en esta población apoyen la legislación. Los números correspondientes de personas representadas por estos porcentajes en la población se pueden calcular multiplicando la población total, 50,000, por 0.32 y por 0.38, lo que da como resultado 50,000(0.32) = 16,000 y 50,000(0.38) = 19,000, respectivamente. De ello se deduce que cualquier valor en el intervalo de 16,000 a 19,000 es un valor plausible para el número total de personas en la población que apoyan la legislación propuesta. De las opciones dadas, solo 16,750 está dentro de este intervalo.
   
   Fuente: College Board, examen de práctica SAT matemáticas.

3. El gráfico muestra el número de barras de chocolate que una determinada máquina envuelve con una etiqueta en x segundos.
   

   

   
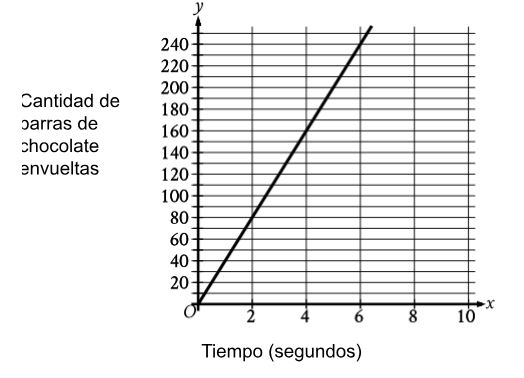
   Según la gráfica, ¿cuál es el número estimado de barras de chocolate que la máquina envuelve con una etiqueta por segundo?
   A. 2
   B. 40
   C. 78
   D. 80
   
   Respuesta: B. Se ve que en 2 segundos envuelve 80 barras. Por ende, en 1 segundo envuelve 40 barras.
   
   Fuente: College Board, examen de práctica SAT matemáticas.

4. Nasir compró 9 contenedores de almacenamiento y cada uno tenía el mismo precio. Usó un cupón para obtener $63 de descuento en toda la compra. El costo de la compra completa después de usar el cupón fue de $27. ¿Cuál era el precio original, en dólares, de 1 contenedor de almacenamiento?
   A. 10
   B. 15
   C. 20
   D. 25
   
   Respuesta: A.
   Dado que el costo de toda la compra fue $27 después de que se utilizó un cupón de descuento por $63 en toda la compra. Sumar el importe del cupón al precio de compra produce 27+63 = 90. Por lo tanto, el costo de toda la compra antes de usar el cupón fue $90. Se da que Nasir compró 9 contenedores de almacenamiento. El precio original de un contenedor de almacenamiento se puede encontrar dividiendo el costo total por 9.
   Por lo tanto, el precio original de un contenedor de almacenamiento es 90/9 =10.
   
   Fuente: College Board, examen de práctica SAT matemáticas.

5. Un camión de mudanzas puede arrastrar un remolque si el peso combinado del remolque y las cajas que contiene no supera los 4,600 kilos. ¿Cuál es la cantidad máxima de cajas que este camión puede transportar en un remolque con un peso de 500 kilos si cada caja pesa 120 kilos?
   A. 34
   B. 35
   C. 38
   D. 39
   
   Respuesta: A
   Si el camión puede remolcar hasta 4.600 kilos y el remolque pesa 500 km. La ecuación es igual a 4.600= 500 + c.120, siendo las cantidades de cajas.
   c= (4600 - 500) /120
   c= 34,16666
   Por lo cual, A sería la respuesta correcta, ya que B se excede del peso máximo.
   
   Fuente: College Board, examen de práctica SAT matemáticas.

6. La estación espacial Mir permaneció en órbita durante 15 años y giró alrededor de la Tierra unas 86 500 veces durante su permanencia en el espacio. La estadía más prolongada de un cosmonauta en la Mir fue de aproximadamente 680 días.
   ¿Aproximadamente cuántas veces voló este cosmonauta alrededor de la Tierra?
   A. 110
   B. 1.100
   C. 11.000
   D. 110.000
   
   Respuesta: C.
   Si un año tiene 365 días, 15 años son igual a 15x365= 5.475 días (se le podrían 3 o 4 días por los años bisiestos, pero no afecta mucho). Para obtener cuantas veces por días giró la estación alrededor de la tierra se divide 86.500 por la cantidad de días equivalente a 15 años. 86.500/5475 = 15,79.
   Si la estadía del cosmonauta duró 680 días y dió aproximadamente 15,79 vueltas por día, giró aproximadamente 680 x 15,79 = 10.737 veces. La respuesta más cercana sería C.
   
   El peso total de la Mir era 143 000 kg. Cuando la Mir volvió a la Tierra, alrededor de un 80% se quemó en la atmósfera. El resto se quebró en unos 1.500 pedazos y cayó al Océano Pacífico.
   ¿Cuál es el peso promedio de los pedazos que cayeron al Océano Pacífico?
   A. 19 kg
   B. 76 kg
   C. 95 kg
   D. 480 kg
   
   Respuesta: A.
   Si el 100% del peso del Mir era 143.000 y se perdió el 80% debemos obtener cuál es el 20% restante. 20x143.000/100=28.600. Suponiendo que los pedazos en promedio son iguales tomamos la cantidad que no se quemo y la dividimos por 1.500.
   28.600/1500= 19,0666
   
   Fuente: PISA, matemáticas, actividades de simulación.

7. En un juego de cartas en particular, la puntuación mínima que un jugador puede lograr en un solo juego es 20 y la puntuación máxima posible en un solo juego es 52. Si un jugador juega tres juegos y obtiene un total de 141 puntos, ¿cuál es el puntaje mínimo que el jugador podría haber marcado en uno de los juegos?
   A. 35
   B. 36
   C. 37
   D. 38
   
   Respuesta: C.
   La menor puntuación posible en un juego se producirá cuando el jugador haya anotado el máximo posible (52 puntos) en cada uno de los otros dos juegos. Estos dos juegos suman 104 puntos, dejando 141 − 104 = 37 puntos como la puntuación más baja posible para el juego restante.
   
   Fuente: Erikthered, SAT examen de práctica sección matemática nivel intermedio

8. Un número de tres dígitos, XYZ, está formado por tres dígitos distintos de cero, X, Y y Z. Si el valor de X es el doble del valor de Z y el valor de Y es tres veces el valor de X, ¿cuál es el número XYZ?
   A. 261
   B. 123
   C. 457
   D. 987
   
   Respuesta: A. Se puede hacer por descarte. Pero se puede probar que 261 es el único número que cumple con esas proporciones. Como Y es el triple que X y X es el doble que Z, Y es 6 veces Z. Si Z fuera más grande que uno, Y sería más grande que 9, el dígito más alto. Por ende, Z es 1, X es 2 y, por último, Y es 6.
   
   Fuente: Erikthered, SAT examen de práctica sección matemática nivel intermedio

9. Un dado estándar es un cubo con entre uno y seis puntos en cada cara. La primera cara tiene un punto, la segunda cara tiene dos puntos, y así sucesivamente. Los puntos están dispuestos de modo que el número total de puntos en cada par de caras opuestas sea 7.
   Todas las siguientes imágenes podrían ser vistas de un dado estándar EXCEPTO:
   

   

   
   
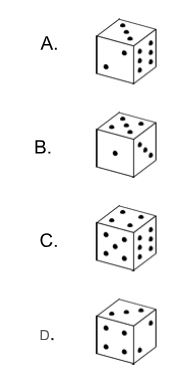
   Respuesta: D. Se ve que el lado con 4 puntos está al lado del lado con 3 puntos. El enunciado aclara que el número total de puntos en cada par de caras opuestas debe ser 7, que sería imposible de lograr en un dado normal si el 4 está al lado del 3.
   
   Fuente: Erikthered, SAT examen de práctica sección matemática nivel intermedio

10. m, 2m, 4m, ...
    El primer término de la secuencia anterior es m, y cada término posterior es igual al doble del término anterior. Si m es un número entero, ¿cuál de los siguientes NO podría ser la suma de los primeros cuatro términos de esta secuencia?
    A. −25
    B. −15
    C. 45
    D. 75
    
    Respuesta: A
    Los primeros cuatro términos son m, 2m, 4m y 8m. La suma de ellos es 15m. Como m es un número entero, 15m debe ser múltiplo de 15. La respuesta A es correcta ya que no es múltiplo de 15.
    
    Fuente: Erikthered, SAT examen de práctica sección matemática nivel intermedio

11. Un autobús viaja a una velocidad constante a lo largo de un tramo recto de la carretera. La ecuación d=30t da la distancia d, en metros desde un marcador de carretera, a la que estará el autobús t segundos después de pasar el mercador. ¿A cuántos metros del marcador estará el autobús 2 segundos después de pasar el marcador?
    A. 30
    B. 32
    C. 60
    D. 90
    
    Respuesta: C
    Si en la ecuación t representa los segundos después de pasar el marcador, para obtener a cuantos metros estará el autobús del marcador 2 segundos después de pasarlo se debe reemplazar 2 en la ecuación donde corresponde a t y así obtener la distancia.
    d=30 x 2
    d=60
    
    Fuente: College Board, examen de práctica SAT matemáticas.

12. Para estimar la proporción de una población que tiene una determinada característica, se seleccionó una muestra aleatoria de la población. Según la muestra, se estima que la proporción de la población que tiene la característica es de 0,49, con un margen de error asociado de 0,04.
    Basado en esta estimación y margen de error, ¿cuál de las siguientes es la conclusión más apropiada sobre la proporción de la población que tiene la característica?
    A. La proporción esté entre 0,45 y 0,53
    B. La proporción es menor que 0,45
    C. La proporción es exactamente 0.49
    D. La proporción es mayor a 0,53
    
    Respuesta: A
    La opción A es correcta. Se da que la estimación de la proporción de la población que tiene la característica es con un margen de error asociado de 0,04. Restando el margen de error de la estimación y sumando el margen de error a la estimación se obtiene un intervalo de valores plausibles para la verdadera proporción de la población que tiene la característica. Por lo tanto, es plausible que la proporción de la población que tiene esta característica esté entre 0,45 y 0,53.
    
    Fuente: College Board, examen de práctica SAT matemáticas.

13. Un objeto viaja a una velocidad constante de 12 centímetros por segundo. A esta velocidad, ¿cuál es el tiempo, en segundos, que le tomara al objetivo viajar 108 centímetros?
    A. 9
    B. 96
    C. 120
    D. 972
    
    Respuesta: A
    Si el objeto viaja 108 centímetros a una velocidad de 12 centímetros por segundo, el tiempo de viaje se puede determinar dividiendo la distancia total por la velocidad. Esto resulta en una regla de tres simple donde
    12 cm = 1 segundo.
    108 cm = x
    108 *1/12 = 9
    
    Fuente: College Board, examen de práctica SAT matemáticas.

14. Theo se pone el objetivo de correr al menos 24 kilómetros cada día para prepararse para un maratón. En un cierto día, Theo planea correr a una velocidad promedio de 4 kilómetros por hora. ¿Cuál es el mínimo de horas que Theo debe correr para cumplir ese día su objetivo diario?
    A. 4
    B. 6
    C. 20
    D. 24
    
    Respuesta: B
    Dado que Theo planea correr a una velocidad promedio de 4 kilómetros por hora y quiere correr 24 km por día, se plantea la regla:
    A.4 km en 1 hora
    B.24 km en x horas
    C.X = 24*1 /4
    D.X = 6
    
    Fuente: College Board, examen de práctica SAT matemáticas.

15. Sebastián alquila una carpa al costo de $11 por día más un seguro de una única vez por $10. ¿Cuál de las siguientes ecuaciones representa el costo total c, en pesos, para alquilar la carpa con el seguro por d días?
    A. c= 11(d+10)
    B. c= 10(d+11)
    C. c= 11d+10
    D. c= 10d+11
    
    Respuesta: C es correcta. El costo del alquiler será el costo por día multiplicado por la cantidad de días más el costo del seguro. Por ende, hay que multiplicar $11 por d (la cantidad de días) y sumarle $10 por el costo del seguro. La ecuación que representa esto es
    c = 11d + 10

16. La longitud, l, de una ballena blanca era 162 cm cuando nació y aumentó un promedio de 4.8 cm por mes los primeros 12 meses después de haber nacido. ¿Qué ecuación representa mejor esta situación, donde x es el número de meses después del nacimiento de la ballena y l es la longitud, en cm , de la ballena?
    A. l = 162x
    B. l = 162x + 162
    C. l = 4.8x + 4.8
    D l = 4.8 x + 162
    
    Respuesta D
    La opción D es correcta. El aumento total en la longitud de la ballena, en centímetros, es 4.8 veces x. La longitud de la ballena, en centímetros, se puede encontrar sumando la longitud de la ballena al nacer, 162 centímetros, al aumento total de longitud. Por tanto, la ecuación que mejor representa esta situación es l = 4.8x + 162
    
    Fuente: College Board, examen de práctica SAT matemáticas.

17. Compro un televisor cuyo precio de vidriera es $57.000 y consigo un descuento del 10% con un voucher. Al llegar a la caja, el cajero me dice que sobre el total, incluyendo el descuento, puede hacerle un descuento del 15% si pago con una tarjeta determinada. ¿A cuánto pagué el total del televisor si pagué con esa tarjeta?
    A. 43.605
    B. 42.750
    C. 40.600
    D. 41.756
    
    Respuesta: A. El subtotal del televisor con el voucher es de 57.000 x 0.9 = $51.300. Sobre este subtotal se aplica el 15% de descuento de la tarjeta, por lo que el precio pagado es 51.300 x 0.85 = $43.605.

18. El número de minutos de luz solar X, y el número de minutos sin luz solar, Y, en un día particular en Las Toninas se relacionan con la ecuación X + Y = 1.440. Si el día tiene 670 minutos de luz solar, ¿cuántos minutos sin luz solar tiene el día?
    A. 670
    B. 770
    C. 1.373
    D. 1.400
    
    Respuesta: B
    Sustituir 670 por X en la ecuación X + Y = 1.440 da como resultado 670 + Y = 1.440. Por lo tanto y = 1440 - 670, produce y = 770. Por lo tanto, este día tiene 770 minutos sin luz diurna.
    
    Fuente: College Board, examen de práctica SAT matemáticas.

19. Victoria seleccionó 20 empleados al azar de los 400 empleados de una empresa. Encontró que 16 de los empleados de esta muestra están inscritos en exactamente tres cursos de desarrollo profesional este año. Según el hallazgo de Victoria, ¿cuál de las siguientes es la mejor estimación del número de empleados de la empresa que están inscritos en exactamente tres cursos de desarrollo profesional este año?
    A. 4
    B. 320
    C. 380
    D. 384
    
    Respuesta: B
    Dado que el 16 es el 80% de 20, se deduce que el 80% de los empleados de la muestra están inscritos en exactamente tres cursos de desarrollo profesional este año. Por lo tanto, la mejor estimación para el porcentaje de empleados de toda la empresa que están inscritos en exactamente tres cursos de desarrollo profesional este año es del 80%. Se indica que la empresa cuenta con un total de 400 empleados. Por lo tanto, la mejor estimación del número de empleados que están inscritos en exactamente tres cursos de desarrollo profesional este año es 320, es decir el 80%.
    
    Fuente: College Board, examen de práctica SAT matemáticas.

20. En una sala de cine hay un total de 350 clientes. Cada cliente está ubicado en el teatro A, el teatro B o el teatro C. Si uno de estos clientes se selecciona al azar, la probabilidad de seleccionar un cliente que esté ubicado en el teatro A es 0,48 , y la probabilidad de seleccionar un cliente que se encuentra en el teatro B es 0,24 . ¿Cuántos clientes se encuentran en el teatro C?
    A. 28
    B. 40
    C. 84
    D. 98
    
    Respuesta: D
    Si el 48% y 24% de los espectadores están en los teatros A y B respectivamente, el 27% restante debe estar en el teatro C. El 27% de 350 es 98.
    
    Fuente: College Board, examen de práctica SAT matemáticas.